Tag Archives: subnetting

IPv6 Subnetting – General Procedure

Posted on by

16

First off, because I know most of us are coming from the IPv4 world, I want to state a couple of things from IPv4 subnetting that we must UNLEARN and forget in order to grasp IPv6 subnetting.

  1. Why we subnet: In IPv4, we usually subnet to conserve addresses (“I can’t waste an entire /24 on a point to point link”). In IPv6 we subnet to optimize our network either for security (“I want all Finance department devices to be on their own subnet”, so we can write simple ACLs for accessing that subnet) or routing (“I want everyone on the same floor or a portion of it to be in the same subnet” – so we can have a single route entry for an entire floor or building thus keeping out routing tables small). Address conservation is not factor in IPv6 subnetting – if you allocate /64s to all your LANs, there’ll always be enough host addresses per subnet.
  2. There is no VLSM, only SLSM: To conserve addresses in IPv4, we use variable length subnet masking (VLSM) – so we’d take a prefix, cut it up and give /30s to point to point links, /25s to small LANs etc. In IPv6, again we don’t need to conserve space, so we assign and use the same prefix lengths (the IPv6 equivalent of a subnet mask) – this will be what we know in the IPv4 world as “same length subnet masking” (SLSM)
  3. Think in terms of subnets and not hosts: Again as we are using /64 subnets, we have enough addresses for hosts so we never really need to calculate the “number of hosts per subnet”. In IPv6 subnetting, we are concerned mostly about the number of subnets.

The general IPv6 subnetting problem has the following variations:

  • Given a specific prefix of length l, how many sub-prefixes of length l’ are there in the given prefix? and what are these prefixes?
  • Given a specific prefix of length l, you are required to break it up to fit a certain number of networks (N)
 

Definitions

  • Mother prefix: this is the prefix that you are going to subnet. It’s prefix length is L. You would get this from the problem set or in practice, as the prefix allocated to you by the RIR or your ISP.
  • Sub-prefixes: these are the component prefixes that you get from subnetting the mother prefix. They have a prefix length (designated L’) such that  L’ > L always. We find the sub-prefix lengths (L’) either directly (e.g. how many /52s are there in the /48 that I got from my ISP?) or from the situation we are facing (I have this /32 prefix that I need to divide equally amongst 700 POPs)
  • Subnet bits (s): in each variation of the IPv6 subnetting problem, you will need to find the number of bits of subnetting needed to give either the sub-prefix length or the number of subnets required.
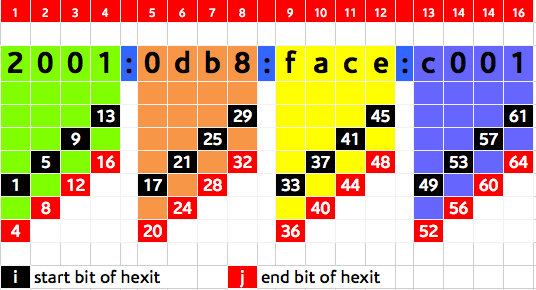
  • Hexit: a single hexadecimal character (0 – 9 , a – f). A hexit is four bit or a nibble.
 

General procedure

[a] Find the number of subnet bits

  • Given both the mother-prefix length and the subnet prefix lengths, then s = L’ – L
  • Given the number of subnets (N), calculate s from the formular 2^s >= N
  • Mathematically, s = log N / log 2 (the answer is rounded up to the next integer)

[b] Find the number of subnet (or interesting) hexits

  • A hexit is a single hexadecimal character and the subnet hexits are those that will change for each of sub-prefixes.
  • Knowing that 1 hexit = 4 bit and having found the number of bits required then
  • Number of subnet hexits = s/4 (round it up to the next integer)
  • Note: If s/4 is an integer, then it means that the hex values for each of the hexits for the last subnet will be “F”.
  • If s/4 leaves a remainder, then the rightmost hexit will not end in something other than an “F”.
  • For simplicity in subnetting and address planning, it is recommended to always work with nibble boundaries (multiples of 4) so that we have clean hexit boundaries.

[c] Find the ‘Increment’ or ‘Block’

This is a constant which is the numerical difference between each of the subnet numbers. Progressive ‘subnet hexits’ are multiples of the ‘Increment’ or ‘Block’

The block B = 2^(16 – L’%16) - the modulo operation % simply takes the remainder and ignores the quotient of the division

[d] Enumerate the subnetIDs

Knowing your subnet prefix length, subnet hexits and block, your subnet IDs form a simple arithmetic progression with initial term 0 and common ratio = Increment

Generally the nth term of an arithmetic progression is: a(n) = a(0) + (n-1)d

Starting from the zeroth subnet i.e. a(0) = 0000 then we have a(n) = (n-1)d

Specifically, to find the last subnetID

  • First find the total number of possible subnets: S = 2^s
  • Last subnetID = a(S) = (S-1)d
  • IMPORTANT! The result above is in decimal so we must convert the result to hex. We an also convert S and d to hex and then work directly in hex.

Our subnets then will be of the general form –  mother:prefix:subnetID::/L’

It is really that simple but “the devil” as they say, “is in the details”. So let’s go search for the devil with an example (and hope he doesn’t demand our souls for the honour):

Worked example

Given the prefix 2001:db8::/32, we need to carve it into 900 sub-prefixes.

This problem gives us the number of required subnets so we’ll have to find the subnet bits. The simpler variation is when we are given the subnet prefix length.

Step #1: Finding the number subnet bits (s) are required

2^s >= 900. So s = (lg 900) / (lg 2) = 10 (rounded up to the nearest integer)

Thus in order to get 900 sub-prefixes, we need at least 10 bits of subnetting. (In fact 10 bits will give us 1024 (2^10) networks but 9 bits will give us 512 which doesn’t meet our requirement)

Now, 10 bits of subnetting means that the sub-prefixes will have a length (L’) of 32 + 10 = 42

Step #2: Finding the number of ‘Subnet Hexits’

Knowing that we need to do 10 bits of subnetting and 4 bits = 1 hexit, then

Therefore 10bits give us 10/4 = 2.5 hexits. We round this to 3 hexits.

The fraction simply means that hexit will vary from 0 and not get through to the top of the hex range i.e. ‘f’

Thus our sub-prefixes will be of the form: 2001:db8:HHH0::/42 (the first two ‘H’s going from 0 – f and the last one ending at some yet-to-be determined value). Again this is another reason to work with nibble (4 bit) boundaries, we avoid all this ‘mess’ and all hexits will change cleanly from 0, 1, 2, 3, 4 … up to f.

Step #3: Finding the Increment (or Block B)

B = 2^(16 – L’%16) = 2^(16 – 42%16) = 2^(16-10) = 2^6 = 64

The hexadecimal equivalent of 64 is 0×40

Step #4: Enumerating the subnetIDs

The general subnetID is given by either one of the following:

  • subnetID(n) = 64(n-1)         [decimal - so we must convert the final result to hex ]
  • subnetID(n’) = 40(n’-1)       [where n' = hex equivalent of n]

Particularly, we want to find the subnetID of the last subnet (we would not need to do this if the subnet prefix fell on a nibble boundry), of which we know there are 1024 (since we calculated that we needed 10 bits to satisfy the design requirement)

So the 1024th subnetID is:

a(1024) = 64(1024 – 1) = 64(1024-1) = 1023(64) = 65472 which in hex is ffc0.

Alternatively, working in hex and knowing that 1024 = 0×400, we could also have

a(400) = 40(400-1) = 3ff(40) = ffc0

So then our last subnetID is : 2001:db8::/42 to 2001:db8:ffc0::/42

We can also find any arbitrary nth subnetID e.g the 243rd one:

a(243) = (243-1)x64 = 242 x 64 = 15488 = 0x3C80 which gives us prefix 2001:db8:3c80::/42 or in hex

a(f3) = 40(f3-1) = 40(f2) = 3C80 which gives us the same answer. [knowing that 243 = 0xf3]

Conclusion and getting real

While I enjoy the intellectual stimulation of knowing how to work this out, I think network engineers should use a good tool to do subnetting in IPv6 after understanding the basics. For a quick technique for doing subnetting of up to 16 subnets in your head, read this post. For anything more complicated, I’d resort to the myriad of tools out there. Apart from the “TheMaskU” iPad app which is really useful, my favorite and preferred is the open source sipcalc. To use these tools well, you need to understand how to find the number of subnet bits and derive the sub-prefix length from it. Our example in sipcalc will be solved as follows:



1


<br />$ sipcalc 2001:db8::/32 --v6split=42 | more<br />-[ipv6 : 2001:db8::/32] - 0<br /><br />[Split network]<br />Network                 - 2001:0db8:0000:0000:0000:0000:0000:0000 -<br /><%%KEEPWHITESPACE%%>                          2001:0db8:003f:ffff:ffff:ffff:ffff:ffff<br />Network                 - 2001:0db8:0040:0000:0000:0000:0000:0000 -<br /><%%KEEPWHITESPACE%%>                          2001:0db8:007f:ffff:ffff:ffff:ffff:ffff<br />Network                 - 2001:0db8:0080:0000:0000:0000:0000:0000 -<br /><%%KEEPWHITESPACE%%>                          2001:0db8:00bf:ffff:ffff:ffff:ffff:ffff<br />Network                 - 2001:0db8:00c0:0000:0000:0000:0000:0000 -<br /><%%KEEPWHITESPACE%%>                          2001:0db8:00ff:ffff:ffff:ffff:ffff:ffff<br />Network                 - 2001:0db8:0100:0000:0000:0000:0000:0000 -<br /><%%KEEPWHITESPACE%%>                          2001:0db8:013f:ffff:ffff:ffff:ffff:ffff<br /><br />Network                 - 2001:0db8:fc80:0000:0000:0000:0000:0000 -<br /><%%KEEPWHITESPACE%%>                          2001:0db8:fcbf:ffff:ffff:ffff:ffff:ffff<br />Network                 - 2001:0db8:fcc0:0000:0000:0000:0000:0000 -<br /><%%KEEPWHITESPACE%%>                          2001:0db8:fcff:ffff:ffff:ffff:ffff:ffff<br />Network                 - 2001:0db8:fd00:0000:0000:0000:0000:0000 -<br /><%%KEEPWHITESPACE%%>                          2001:0db8:fd3f:ffff:ffff:ffff:ffff:ffff<br />Network                 - 2001:0db8:fd40:0000:0000:0000:0000:0000 -<br /><%%KEEPWHITESPACE%%>                          2001:0db8:fd7f:ffff:ffff:ffff:ffff:ffff<br />Network                 - 2001:0db8:fd80:0000:0000:0000:0000:0000 -<br /><%%KEEPWHITESPACE%%>                          2001:0db8:fdbf:ffff:ffff:ffff:ffff:ffff<br />Network                 - 2001:0db8:fdc0:0000:0000:0000:0000:0000 -<br /><%%KEEPWHITESPACE%%>                          2001:0db8:fdff:ffff:ffff:ffff:ffff:ffff<br />Network                 - 2001:0db8:fe00:0000:0000:0000:0000:0000 -<br /><%%KEEPWHITESPACE%%>                          2001:0db8:fe3f:ffff:ffff:ffff:ffff:ffff<br />Network                 - 2001:0db8:fe40:0000:0000:0000:0000:0000 -<br /><%%KEEPWHITESPACE%%>                          2001:0db8:fe7f:ffff:ffff:ffff:ffff:ffff<br />Network                 - 2001:0db8:fe80:0000:0000:0000:0000:0000 -<br /><%%KEEPWHITESPACE%%>                          2001:0db8:febf:ffff:ffff:ffff:ffff:ffff<br />Network                 - 2001:0db8:fec0:0000:0000:0000:0000:0000 -<br /><%%KEEPWHITESPACE%%>                          2001:0db8:feff:ffff:ffff:ffff:ffff:ffff<br />Network                 - 2001:0db8:ff00:0000:0000:0000:0000:0000 -<br /><%%KEEPWHITESPACE%%>                          2001:0db8:ff3f:ffff:ffff:ffff:ffff:ffff<br />Network                 - 2001:0db8:ff40:0000:0000:0000:0000:0000 -<br /><%%KEEPWHITESPACE%%>                          2001:0db8:ff7f:ffff:ffff:ffff:ffff:ffff<br />Network                 - 2001:0db8:ff80:0000:0000:0000:0000:0000 -<br /><%%KEEPWHITESPACE%%>                          2001:0db8:ffbf:ffff:ffff:ffff:ffff:ffff<br />Network                 - 2001:0db8:ffc0:0000:0000:0000:0000:0000 -<br /><%%KEEPWHITESPACE%%>                          2001:0db8:ffff:ffff:ffff:ffff:ffff:ffff<br /><br />

Calculating IPv4 Summary Prefixes

Posted on by

5

Given a list of IPv4 prefixes of the same length, how do you find the summary address (or addresses) for them? This post describes a method and uses some worked examples to illustrate. The post draws deeply from the CCIE Routing and Switching Exam Certification Guide by Wendel Odom, with lots additions of mine for clarity as well as some procedures that are not described in the text. I assume that you already understand the standard terminology associated with IPv4 addressing in general.

Definitions

  • Block (B): Different subnet numbers are multiples of the block (B).
  • The block for prefix length (P) is given by: B(P) = 2^{8-P\%8}.
  • The modulo (MOD or %) operation simply finds the remainder of dividing one number by another. We are dividing by 8 here because each octet of an IPv4 address is 8 bits in length.
  • Inclusive summary address: A summary that includes prefixes outside the range of prefixes you are summarizing.
  • Exclusive summary address: A summary address (or addresses in some cases) that only includes prefixes within the range you are summarizing.
  • Interesting Octet: the octet within the IPv4 address in which the prefix length falls. To find this, simply divide the prefix length by 8 and round to the next whole integer.

General procedure

The general procedure to find the exclusive summary address(es) is as follows:

  1. Find the inclusive summary route and use this as the first candidate exclusive address.
  2. Determine the range of addresses of the candidate exclusive address. If it totally encompasses all the component prefixes, then this candidate is the exclusive summary address. If not, split the component candidate address into two with a new prefix length P’ = P + 1
  3. Repeat step #2 for each half of the candidate summary address. As you do this several times, you will eliminate prefixes from the bottom and top of the range till you are left with just the exact prefixes that encompass all the candidate prefixes.

Calculating the inclusive summary route

You should know (from your routing table) or from the problem set in an exam the following information

  • A list of prefixes to summarize i.e. the component prefixes.
  • The prefix length of the prefixes (P). This is the same for all component prefixes.

You use the given prefixes to find the inclusive summary route as follows:

  1. Let the number of component prefixes be ‘s’
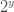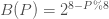  2. The number of bits required to give ‘s’ prefixes is given by ‘y’ where: 2^{y} ≧ s (take the next whole integer)
  3. Calculate a new prefix length P’ = P – y
  4. Calculate S0 – the subnet number when you take the lowest numeric subnet (e.g 192.168.20.0 is less than 192.168.25.0) in the list as an IP address with prefix length P’.
  5. Calculate S1 – the subnet number when you take the highest numeric subnet in the list as an IP address with prefix length P’
  6. If S0=S1 then this is the best summary route.
  7. If S0≠S1, then repeat steps #4 and #5 with a new (shorter) prefix length P’= P’ – 1

Calculating the exclusive summary route

  1. Find the inclusive summary prefix and use it as a candidate exclusive summary prefix
  2. Determine the range of the candidate summary, if all candidates prefixes fall within the range, then this is the exclusive summary prefix and you are done.
  3. If the range of the candidate prefixes includes prefixes outside the component prefixes, split the candidate into two parts with length P’ = P +1 and repeat step #2 with each half.

How to split a prefix into two parts

  1. Find the new prefix length: P’ = P + 1
  2. Calculate the block that corresponds to this new prefix length B(P’)
  3. First part = candidate prefix
  4. Second part = candidate prefix + B(P’) on the interesting subnet

Worked Example #1 : Inclusive summary route

Find the inclusive summary prefix for: 172.31.20.0/24, 172.31.21.0/24, 172.31.22.0/24, 172.31.23.0/24

  • Number of prefixes s = 4
  • Prefix length of components P = 24
  • Bits required y: 2^y >= s => 2^y >=4 thus y = 2
  • New prefix length P’ = P – y = 24 – 2 = 22

Taking smallest component prefix as an address with new prefix length, we have 172.31.20.0/22

  • Block B(22) = 2^(8-22%8) = 2^2 = 4
  • Thus subnet number are multiples of 4 i.e. 4 , 8 , 12, 16, 20 , 24, etc
  • Interesting octet is 3rd octet (22/8 = 2R6 = 3)
  • This address belongs to subnet 172.31.20.0/22 = S0

Taking the highest component prefix as an address with new length, we have 172.31.23.0/22

  • Block B(22) = 2^(8-23%8) = 2^2 = 4
  • Thus subnet number are multiples of 4 i.e. 4 , 8 , 12, 16, 20 , 24, etc
  • Interesting octet is 3rd octet (22/8 = 2R6 = 3)
  • This address belongs to subnet 172.31.20.0/22 = S1

S0 = S1 thus the inclusive summary prefix is 172.31.20.0/22

Worked Example #2 : exclusive summary route

Find the exclusive summary of 172.31.20.0/24, 172.31.21.0/24, 172.31.22.0/24, 172.31.23.0/24 ,172.31.24.0/24

We start of by finding the inclusive summary prefix first and using it as a candidate exclusive summary prefix.

  • Number of prefixes s = 5
  • Prefix length of components P = 24
  • Bits required y: 2^y >= s => 2^y >=5 thus y = 3
  • New prefix length P’ = P – y = 24 – 3 = 21
  • Block B(21) = 2^(8-21%8) = 2^3 = 8
  • Thus subnet number are multiples of 8 i.e. 8 , 16 , 24, 32 etc
  • Interesting octet is 3rd octet (21/8 = 2R5 = 3)

Taking smallest component prefix as an address with new prefix length, we have 172.31.20.0/21 which belongs to subnet 172.31.16.0/21 = S0

Taking the highest component prefix as an address with new length, we have 172.31.24.0/21, which belongs to subnet 172.31.24.0/21 = S1

S0 ≠ S1 we repeat with prefix length decremented by 1

  • New prefix length P’ = P’ – 1 = 21 – 1 = 20
  • Block B(20) = 2^(8-20%8) = 2^4 = 16
  • Thus subnet number are multiples of 16 , 32 , 48 etc
  • Interesting octet is 3rd octet (20/8 = 2R4 = 3)

Taking smallest component prefix as an address with new prefix length, we have 172.31.20.0/20 which belongs to subnet 172.31.16.0/20 = S0

Taking the highest component prefix as an address with new length, we have 172.31.24.0/20 which belongs to subnet 172.31.16.0/20 = S1

S0 = S1 = 172.31.16.0/20 is the inclusive summary prefix

Now that we have the inclusive summary prefix, we can proceed to find the exclusive prefix using this as our first candidate.

First we establish the range of 172.31.16.0/20

  • We know block is B(20) = 16 and the third octet is the interesting one
  • The next subnet higher than 172.31.16.0/20 is 172.31.32.0/20
  • Therefore range of 172.31.16.0/20 is 172.31.16.1 – 172.31.31.255 (this being the last address before 172.31.32.0/20)
  • This range includes more prefixes than are in the component list (e.g .16.0/24 and .28.0/24)

We split 172.31.16.0/20 into two parts

  • New prefix length P’= P’ + 1 = 20 + 1 = 21
  • B(21) = 8
  • Thus 172.31.16.0/20 = 172.31.16.0/21 & 172.31.24.0/21
Split #1 172.31.16.0/21 172.31.24.0/21
Range 172.31.[16.1 - 23.255] 172.31.[24.1 - 31.255]
Comments
  • Includes .16.0/24 so we’ll need to split this again
  • Only 24.0/24 is within range
  • Thus 172.31.24.0/24 is one of the exclusive summary prefixes

Note: We use the block (B) to determine the component subnets and thus know what prefixes are included that shouldn’t be.

We split 172.31.16.0/21 into two parts

  • New prefix length P’= P’ + 1 = 21 + 1 = 22
  • B(22) = 4
  • Thus 172.31.16.0/21 = 172.31.16.0/22 & 172.31.20.0/22
Split #1 172.31.16.0/22 72.31.20.0/22
Range 172.31.[16.1 - 19.255] 172.31.[20.1 - 23.255]
Comments Totally out of range, so we discard this Includes the remaining component prefixes apart from .24.0/24

Therefore, the exclusive summary prefixes for 172.31.[20-24].0/24 are 172.31.20.0/22 AND 172.31.24.0/24

Worked Example #3 : Exclusive summary route

Find the exclusive summary prefix for 10.22.12.0/23, 10.22.14.0/23, 10.22.16.0/23 10.22.18.0/23

We start of by finding the inclusive summary prefix first and using it as a candidate exclusive summary prefix.

  • Number of prefixes s = 4
  • Prefix length of components P = 23
  • Bits required y: 2^y >= s => 2^y >=4 thus y = 2
  • New prefix length P’ = P – y = 23 – 2 = 21
  • Block B(21) = 2^(8-21%8) = 2^3 = 8
  • Thus subnet number are multiples of 8 i.e. 8 , 16 , 24, 32 etc
  • Interesting octet is 3rd octet (21/8 = 2R5 = 3)

Taking smallest component prefix as an address with new prefix length, we have 10.22.12.0/21 which belongs  to subnet 10.22.8.0/21 = S0

Taking the highest component prefix as an address with new length, we have 10.22.18.0/21 which belongs to subnet 10.22.16.0/21 = S1

S0 ≠ S1 we repeat with prefix length decremented by 1

  • New prefix length P’ = P’ – 1 = 21 – 1 = 20
  • Block B(20) = 2^(8-20%8) = 2^4 = 16
  • Thus subnet number are multiples of 16 , 32 , 48 etc
  • Interesting octet is 3rd octet (20/8 = 2R4 = 3)

Taking smallest component prefix as an address with new prefix length, we have 10.22.12.0/20 which belongs to subnet 10.22.0.0.0/20 = S0

Taking the highest component prefix as an address with new length, we have 10.22.18.0/20 which belongs to subnet 10.22.16.0.0/20 = S1

Still, S0 ≠ S1 we repeat with prefix length decremented by 1

  • New prefix length P’ = P’ – 1 = 20 – 1 = 19
  • Block B(19) = 2^(8-19%8) = 2^4 = 32
  • Thus subnet number are multiples of 32 , 64, etc
  • Interesting octet is 3rd octet (19/8 = 2R4 = 3)

Taking smallest component prefix as an address with new prefix length, we have 10.22.12.0/19 which belongs to subnet 10.22.0.0.0/19 = S0

Taking the highest component prefix as an address with new length, we have 10.22.18.0/19 which belongs to subnet 10.22.0.0.0/20 = S1

S0 = S1 = 10.22.0.0/19 is the inclusive summary prefix

Now that we have the inclusive summary prefix, we can proceed to find the exclusive prefix using this as our first candidate.

First we establish the range of 10.22.0.0/19

  • We know block is B(19) = 32 and the third octet is the interesting one
  • The next subnet higher than 10.22.0.0/19 is 10.22.32.0/19
  • Therefore range of 10.22.0.0/19 is 10.22.0.1 – 10.22.31.255 (this being the last address before 10.22.32.0/19)
  • This range obviously includes more prefixes than are in the component list so we split it

We split 10.22.0.0/19 into two parts

  • New prefix length P’ = P’ + 1 = 19 + 1 = 20
  • B(20) = 16
  • Thus 10.22.0.0/19 —> 10.22.0.0/20 & 10.22.16.0/20
Split #1 10.22.0.0/20 10.22.16.0/20
Range 10.22.[0.1 - 15.255] 10.22.[16.1 - 31.255]
Comments Includes ranges below 10.22.12.0/24
  • Includes ranges above 10.22.18.0/24
  • We’ll need to split this to trim the range from above

We split 10.22.0.0/20 into two parts

  • New prefix length P’= P’ + 1 = 20 + 1 = 21
  • B(21) = 8
  • Thus 10.22.0.0/20 –> 10.22.0.0/21 & 10.22.8.0/21
Split #2 10.22.0.0/21 10.22.8.0/21
Range 10.22.[0.1 - 7.255] 10.22.[8.1 - 15.255]
Comments Totally out of range
  • Includes the .12.0, 14.0 and 16.0 prefixes
  • Still includes the prefixes below .12.0 and so needs to be split this prefix to trim it from the bottom

We split 10.22.8.0/21 into two parts

  • New prefix length P’= P’ + 1 = 21 + 1 = 22
  • B(22) = 4
  • Thus 10.22.8.0/21 –> 10.22.8.0/22 & 10.22.12.0/22
Split #3 10.22.8.0/22 10.22.12.0/22
Range 10.22.[8.1 - 11.255] 10.22.[12.1 - 15.255]
Comments Totally out of range  Contains the .12, .14 prefixes and nothing else

We split 10.22.16.0/20 from split #1 into two parts

  • New prefix length P’= P’ + 1 = 20 + 1 = 21
  • B(21) = 8
  • Thus 10.22.16.0/20 –> 10.22.16.0/21 & 10.22.24.0/21
Split #4 10.22.16.0/21 10.22.24.0/21
Range 10.22.[16.1 - 23.255] 10.22.[24.1 - 31.255]
Comments
  • Contains .16.0 and .18.0 but also .20 which we don’t want
  • Split this again
 Totally out of range – discard

We split 10.22.16.0/21 from split #4 into two parts

  • New prefix length P’= P’ + 1 = 21 + 1 = 22
  • B(22) = 4
  • Thus 10.22.16.0/21 –> 10.22.16.0/22 & 10.22.20.0/22
Split #5 10.22.16.0/22 10.22.20.0/22
Range 10.22.[16.1 - 19.255] 10.22.[20.1 - 23.255]
Comments Contains only .16.0 and .18.0 Totally out of range – discard

Therefore, the exclusive summary prefixes for 10.22.[12, 14 , 16, 18].0 /23 are 10.22.12.0/22 AND 10.22.16.0/22

Conclusion

  1. Be aware that when you summarize to certain prefix lengths, some operators might not accept them. Inefficient summary routes lead to bigger BGP tables.
  2. Most ISPs and Regional Internet Registries (RIRs) will allocate you address space along boundaries that can easily be summarized neatly
  3. The Block (B) will always increase in the progression: 2 , 4, 8, 16 , 32 , 64 , 128

IPv6 Subnetting Made Easy

Posted on by

46

Introduction

Call it emotional attachment to IPv4 or whatever you like, but recently I have become more and more interested in finding and easy way to subnet IPv6 prefixes in my head like we are used to doing in IPv4. This post expands on an idea I picked off of the NANOG mailing list.

The method presented here is for the quick subnetting in your head, which you should get by practice. So it works well for a small number of subnets (16 max) but can be expanded for any number of subnets. However if you have to deal with more than 16 subnets, it is certainly more efficient to use any of the several IPv6 calculators out there (my favourite is sipcalc – a command line tool).

This method helps you answer the question: “Given the prefix PPPP/Y, what are the sub-prefixes of length /Z (where Z > Y) that can be gotten from it?“

I assume that you understand the fundamentals of IPv6 addressing, very basic binary and hex math. I also assume that you know how to arrive at the value Z from an analysis of your network design or requirements.



Definitions




    

  • Hexit – a single hexadecimal digit (0 – 9 , a – e). A hexit is made up of 4 bits.
    • 

  • Hex grouping – each of the groups of hexits of an IPv6 address that are separated by colons.
    • 

  • Defining hexit – the hexits that change for each subnet but stays 
the same for the same subnet. Think ‘interesting octet’ from IPv4 
subnetting days. You could simply look it up from the following table.
    • 





The bit ranges that define various IPv6 hexits




    

  • Parent prefix – the original prefix to be subnetted in prefix/length format.
    • 

  • Y = prefix length of original prefix
    • 

  • Z = prefix length of subnets of original prefix
    • 





The Procedure




Calculate the following parameters


    

  1. 

    Number of subnetting bits:  x = Z – Y
    

    2. 

  2. 

    Number of subnets possible with x bits: S = 2^x
    

    3. 

  3. 

    Number of hexits represented by the x bits: h = x/4 (this should be rounded up to the next integer)
    

    4. 



For a given number of subnet bits (x), 
the defining hexit for each subnet will increase in value according to 
the increment, from hexadecimal zero (0) to “e” as shown in the table 
below. Note that the ‘definining’ hexit(s) is simply the one after the 
boundary hexit (that defined by original prefix length Y.



IPv6 Quick Subnetting Cheatsheet
IPv6 Quick Subnetting Cheatsheet




Examples




[a] Subnet 2001:db8::/32 into /36s


    

  • 

    Subnetting bits (x) = 36 – 32 = 4 (these will give us 16 [i.e. 2^4] subnets.
    

    • 

  • 

    Number of hexits represented by 4 bits = 4/4 = 1
    

    • 

  • 

    From the table, the defining hexit should increment by 1 with discrete hex values 0 – f.
    

    • 

  • 

    Thus our subnets are:
    

    • 





2001:db8:0000::/36
2001:db8:1000::/36
2001:db8:2000::/36
2001:db8:3000::/36
2001:db8:4000::/36
2001:db8:5000::/36
2001:db8:6000::/36
2001:db8:7000::/36
2001:db8:8000::/36
2001:db8:9000::/36
2001:db8:a000::/36
2001:db8:b000::/36
2001:db8:c000::/36
2001:db8:d000::/36
2001:db8:e000::/36
2001:db8:f000::/36




[b] As a small end site, you received the 2001:db8:c001:ba00::/56 
assignment from your ISP, and you have 3 main office locations you want 
to divide this block between. Find these 3 subnets.


    

  • 

    Number of subnets required = 3
    

    • 

  • 

    Subnetting bits (x) such that (2^x)
 >=3 , x = 2 (this will actually give us 4 subnets of equal prefix 
length). Also the prefix length of our subnets will be 58 (56+2)
    

    • 

  • 

    Number of hexits represented by 2 bits = 1
    

    • 

  • 

    From the table, the defining hexit should increment by 4 with discrete hex values 0, 4, 8, c.
    

    • 

  • 

    Thus our subnets are:
    

    • 





2001:db8:c001:ba00::/58
2001:db8:c001:ba40::/58
2001:db8:c001:ba80::/58
2001:db8:c001:bac0::/58




Please drop me a comment if you have suggestions of how to make 
this even easier and happy v6 subnetting …in your head. If you would 
like a highly detailed and complete method for IPv6 subnetting, let me 
invite you to read my other post “IPv6 Subnetting – General Procedure“